EVOLUÇÃO DO PENSAMENTO FILOSÓFICO E CIENTÍFICO

UNIVERSIDADE FERDERAL DO ESPIRITO SANTO – UFES

LICENCIATURA EM FILOSOFIA - EAD

Disciplina: Evolução do Pensamento Filosófico e Científico

Alunos (as): Maria Telma Jardim Paixão; Larissa Fernandes Coimbra; Luana Ribeiro Silva Lacerda; Vera Lúcia Nunes Moreira Oliveira e Willias Farias Bastos.

PODEM AS MÁQUINAS PENSAR?

1. Ciência, filosofia e Inteligência Artificial

Apesar de haver várias respostas diferentes à possibilidade das máquinas pensarem, dois argumentos já são considerados tradicionais nesse debate: o primeiro, baseado no teste de Turing (Turing Test), afirma que - em certa medida - é possível que máquinas pensem. Oposto ao argumento de Turing se encontra uma tese que foi estabelecida inicialmente pelo filósofo John Searle (1932), conhecida como o “Quarto Chinês” (chinese room).

1.1 A máquina de Turing e o modelo de mente

De acordo com Murta e Mulinari “Alan Mathison Turing (23 de junho de 1912 — 7 de junho de 1954) foi um matemático, lógico, crip¬oanalista e cientista da computação britânico.” (p. 01)

Em 1936 Turing escreve um artigo com o seguinte titulo: “On Computable Number, with an Applicatin to the Entscheidun¬gsproblem”, neste artigo ele busca formalização matemática da noção de máquina, que posteriomente ficou conhecido como “máquina de Turing”. Essa máquina criada por ele teve papel importante na criação do computador moderno que conhecemos hoje.

Com a formalização Turing defende a tese que: “[...] todo procedimento mecânico é modelizável por meio de uma máquina de Turing; ou, já que esses procedimentos são “funcionais” e que se trata, em definitivo, de cálculo: toda função calculável mecanicamente é calculável por uma máquina de Turing” (DUPUY, 1996, p. 36). (p. 01)

A noção básica de uma máquina de Turing é bastante simples. É um recurso que consiste de um mecanismo para fazer uma marca num rolo de fita, que funciona como uma memória para o sistema. O mecanismo pode realizar apenas quatro tipos de operações: pode fazer uma marca; pode remover um marca; pode avançar a fita; pode rebobinar a fita. A própria fita é dividida em segmentos (ou “células”), cada uma das quais pode ou não ser marcada e deve ter duração ilimitada. Não importa quanta fita usamos, há sempre mais (Fetzer, 2001, p.51). (p. 02)

Essa maquina foi criada com fins lógicos matemáticos, mas conforme os autores deste texto hoje é nítida a importância que este experimento teve para os problemas filosóficos, em relação entre a matéria e o pensamento, conhecido também como problema da mente-corpo.

Vale destacar que a máquina Universal de Turing “é que, embora seja uma máquina simples, ela possui uma enorme potência computacional, ao ponto de poder imitar qualquer sistema formal, desde que esse seja formado por uma coleção de elementos arbitrários e regras para sua manipulação. Assim, a diferença entre um computador atual e uma máquina de Turing seria apenas de design, e não de potência. É aqui que as noções de máquina e de mente se aproximam de forma crucial.” (p. 03)

“Em filosofia da mente, o funcionalismo é um conjunto de teses que defende a análise do comportamento e fenômenos mentais segundo as funções que desempenham. Portanto a corrente funcionalista da filosofia da mente toma, em geral, a mente como o modelo da faculdade de modelizar. Uma vez que se tem uma máquina de Turing singular, essa corresponderia a uma faculdade da mente”.

É importante ressaltar que “entusiasmo dos filósofos da época de Turing se dava principalmente devido à hipótese de que a mente poderia ser um recurso computacional, tal como a máquina de Turing. Assim, a teoria de computabilidade defendida por Turing estabeleceria os limites do pensamento, pois todo tipo de pensamento seria, sob certo aspecto, computacional e modelizável. Teríamos, para esses entusiastas, um modelo unificado de mente para longe das disputas filosóficas entre dualistas e materialistas.” (p. 03).

1.2  O jogo da imitação de Turing

Ele também escreveu outro artigo, na qual, foi.” intitulado Computing Machinery and Intelligence (1950). Neste artigo, Turing propõe um modo de solução para a questão sobre pensamento e máquinas (‘podem máquinas pensar?’). 2 A solução de Turing ficou tradicionalmente conhecida como “o jogo da imitação” (The imitation game”.

O jogo da imitação proposto por Turing funciona da seguinte forma: o jogo tem a participação de, um homem, uma mulher e um interrogador, que pode ser de qualquer sexo. O interrogador permanece num espaço separado dos outros dois e se comunica com eles por meio de algum recurso, tais como uma máquina de teletipo, que não entregará o jogo. O objetivo do jogo é que o interrogador decida quem é o homem e quem não é. Os embaraços impostos pelas regras tornam necessário que o interrogador chegue a sua suposição somente com base nas respostas dadas às suas questões (FETZER, 2001, p. 53-54).” (p. 04)

Assim, estabelecido os fundamentos básicos do jogo, existem ainda algumas regras auxiliares:

 Ex: “É permitido ao homem que minta, porém é ordenado à mulher que ela sempre responda com a verdade.”

Na minha humilde opinião por mais que uma máquina simule respostas corretas sobre o comportamento humano, isso não significa que a máquina esteja pensando.

Os autores afirmam que embora exista semelhança ou até mesmo identidade nas respostas é uma ideia bastante plausível. Porém, o que parece ficar em aberto no jogo proposto por Turing é se é possível deduzir da semelhança de resposta dos participantes a conclusão de que ambos possuem sistemas computacionais de operação. Noutras palavras, podemos até concluir que as respostas são semelhantes, mas não parece ser tão simples afirmar que o processo que adotamos para dar essas respostas seja o mesmo que o de uma máquina.” (p. 04)

1.3 O quarto chinês

John Rogers Searle (Denver, 31 de julho de 1932) é um filósofo e escritor norte-americano, professor da Universidade de Berkeley, na Califórnia, Estados Unidos.

Com o ‘quarto chinês’ o filosofo John Searle contra-argumenta os funcionalistas que tomaram como fundamento o jogo da imitação proposto por Turing. “Searle questiona: se uma máquina pode simular convincentemente uma conversa humana, a máquina necessariamente entende o que se passa? Para responder essa questão, o filósofo propõe o experimento denominado “Quarto Chinês” (Chinese Room).” (p. 05)

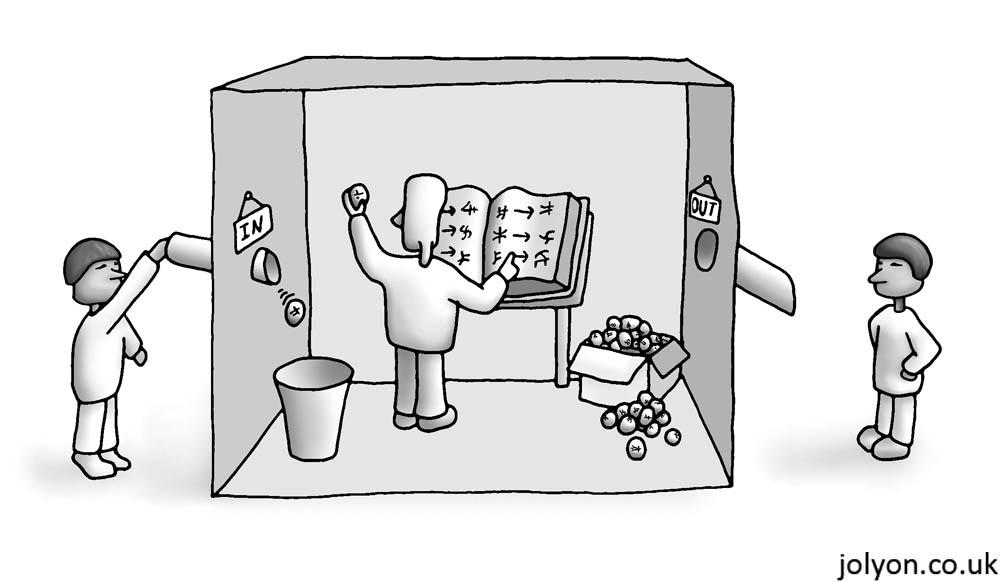
Os autores explicam a questão do “experimento de pensamento é o seguinte. Searle é um falante de inglês que não compreende nada de chinês e está trancado dentro de um quarto. Searle recebe algumas tiras de papel escritas em chinês por meio de uma abertura. Apesar de não compreender o que está escrito, Searle tem acesso a um livro que contém um conjunto de regras, escrito em inglês, que correlaciona a tira de papel que ele recebeu a outro conjunto de tiras de papel, também escritas em chinês, que está à sua disposição no interior do quarto. As instruções do livro são do tipo “ao receber a tira contendo X, coloque pela abertura da porta a tira contendo Y”. Vale a pena ressaltar que tanto X como Y são mensagens com caracteres em chinês e que Searle só entende a instrução, escrita em inglês, que correlaciona X com Y. A correlação entre o símbolo recebido e o símbolo enviado é puramente formal, isto é, Searle os identifica unicamente pelos seus formatos (LIMA FILHO, 2010, p. 54). (p. 05)

Por mais que haja um desempenho computacional ao responder as “questões em chinês tenha passado no Teste de Turing, ou seja, tenha convencido um chinês que a máquina é um falante da língua chinesa. A questão que Searle propõe é, então, a seguinte: a máquina literalmente “compreendeu” chinês? Ou ela meramente simulou a habilidade de entender a língua chinesa?” (p. 05)

 

Searle (1980, p. 2) escreve que de acordo com a Inteligência Artificial forte, a simulação realmente é a mente e, assim, a máquina literalmente entendeu chinês. Porém, de acordo com a Inteligência Artificial Fraca, a simulação correta é apenas um modelo da mente. (p. 06)

Analisando o modelo de máquina de Turing e o contra-argumento de Searle, acredito que as máquinas apenas replicam as respostas dadas pelos seres humanos, mas daí afirmar que elas pensam é outra coisa completamente diferente. Por mais que uma máquina replique essas respostas jamais podemos afirmar que elas pensam.

Conclusão

Neste blog buscamos introduzir o leitor na discussão em torno da questão sobre a possibilidade das maquinas pensarem. O objetivo é apresentar a posição do lógico-matemático britânico Alan Turing, principalmente sua proposta mostrada em seu “jogo da imitação” (The imitation game) e que serve de base para boa parte dos teóricos da inteligência artificial. Também foi apresentado como contraponto o argumento do filosofo John Searle Pautado em seu argumento do “quarto chinês”, que se constitui como uma dura crítica a visão de Turing sobre a possibilidade de máquinas pensarem.

Essas duas visões são as mais tradicionais no debate sobre a possibilidade de máquinas pensarem ou sobre inteligência artificial e também sobre teoria computacional. Começamos então a perceber que quando envolvemos ciências e sobre tudo inteligência artificial, estamos em contato com uma área cientifica na qual a filosofia ainda tem grande respaldo.

Podem as máquinas pensar? Para Turing sim, para Searle não. Eles não são os únicos que dão respostas para esta questão, mas independente das respostas, o que temos certeza é que a computação e a inteligência artificial estão cada vez mais presentes no nosso dia a dia, avançando cada vez mais.

Referências

MULINARI, Felício; MURTA, Cláudia. Podem as máquinas pensar? Vitória: SEAD/UFES, 2017.

Indicações de vídeos e filme: